Creation of Autonomous Artificial Intelligent Agents using Novelty Search method of fitness function optimization

For billions of years of evolution, biological intelligent agents have mastered the power to find optimal solutions in deceptive environments that we encounter in our daily interactions with the real world. We can easy navigate themselves through the maze of a big city subways and roadways. But for artificial intelligent systems, this is too difficult to be easily solved using the optimal computing resources. This is especially true for offline autonomous agents that are not backed by super power of cloud servers.

The main problem here is related to the fact that reliable maze navigation requires the development of a solution in an environment having many traps with strong local optima of fitness function. Such traps are represented as cul-de-sacs that are close to the final destination, but that can not be escaped without a step back, away from the ultimate goal (at least temporary). In such environments, objective-based solvers basically can not find optimal solution or any solution at all, because they do not have the necessary internal machinery for committing the leap-of-faith and move backward from the target in order to eventually find a way out.

The objective-based solvers depends on the best attempts of their designers to assess the operating environment and develop a better way to achieve the ultimate goal. But, as it happens in the real world, preliminary assumptions often can not account for all the traps on the way to the goal because of the extreme complexity of the environment settings. And even in simple artificial environments, such as maze navigation, it often happens that objective-based solvers can not find the optimal solution within the adequate execution time and computational resources allocation. But for successful autonomous execution in real world environments, it is critically important to create Intelligent Agents capable of quickly finding a solution with minimal computational load.

EXPERIMENT OVERVIEW

In the experiment we studied how Novelty Search (NS)¹ method of fitness function optimization performs compared to traditional objective-based ones for unsupervised training of Artificial Intelligent Agents to do spatial navigation in complex maze environment. The main idea behind NS optimization is to rather look for novel outcomes in the search space than the distance to the final objective: the maze exit. The Novelty Search assigns higher fitness values to the Intelligent Agent capable to find the most novel solution among all previous tries. Despite its ignorance to the final objective the NS happens to be extremely effective optimization method capable of breeding AAIA, which crack deceptive real-world tasks even in the realms where traditional objective-based methods have failed completely. The main assumption about what makes this possible, is that in order to reach final goal, AAIA must find several intermediate goals (stepping stones) which in most cases do not resemble the ultimate objective. Sometimes Intelligent Agent must step back to avoid deceptive traps. By doing this it will see a decrease in value of objective-based fitness function for a moment but will get a better outcomes in the future. This is one of the fundamental properties of the real-world environment that the exact route to the final objective in most cases can not be predicted in advance, and all intermediate stepping stones should be found by taking the path.

The Novelty Search optimization seems like a natural fit for Neuro-evolution family of genetic algorithms producing elegant custom Artificial Neural Networks (ANNs). In the experiment we combined NS with Neuroevolution of Augmented Topologies algorithm² which efficiently evolve ANNs through complexification by augmenting its topologies.

More details about NEAT algorithm implementation can be found in my previous article: ‘Neuroevolution — evolving Artificial Neural Networks topology from the scratch’³

> The Maze Solver Agent Configuration

Autonomous Artificial Intelligent Agent, designed to solve the maze, has ten input sensors that allow collecting information about the environment and two output effectors controlling its movements through the maze (see Figure 1). The final objective of the agent is to go through the maze and find a way out.

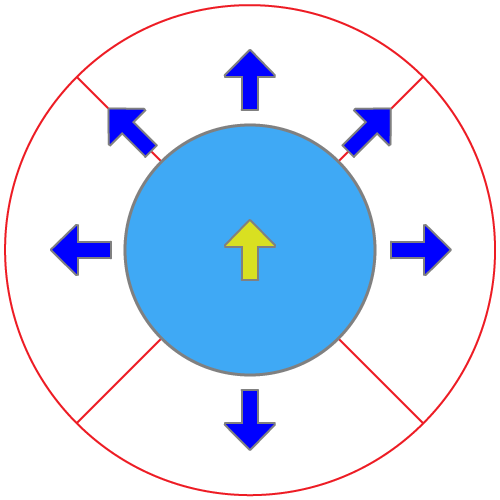
The input sensors are: six range finders that indicate the distance to the nearest obstacle (blue arrows) and four pie-slice radar sensors (slices of red circle) that act as a compass towards the goal (maze exit), activating when a line from the goal to the center of the agent falls within the pie-slice. The green-yellow arrow in the center points to the movement direction of the agent.

The agent is also equipped with two effectors producing a forces that respectively turn and propel the robot, i.e. change its linear and angular velocity.

> Seed Genome Configuration

The configuration of the seed genome of the solver agent can be summarized as follows (see Figure 2):

• ten input (sensor) neurons (blue): six for range finders [RIGHT, FRONT-RIGHT, FRONT, FRONT-LEFT, LEFT, BACK] plus four for slice radar sensors with 45 degree FOV [FRONT, LEFT, BACK, RIGHT]
• two output (effectors) neurons (red): angular (neuron #13) and linear (neuron #14) velocity controlling effectors
• one hidden neuron (#12) to introduce non linearity (green)
• one bias neuron (#1) to avoid zero saturation when input neurons is not activated (yellow)

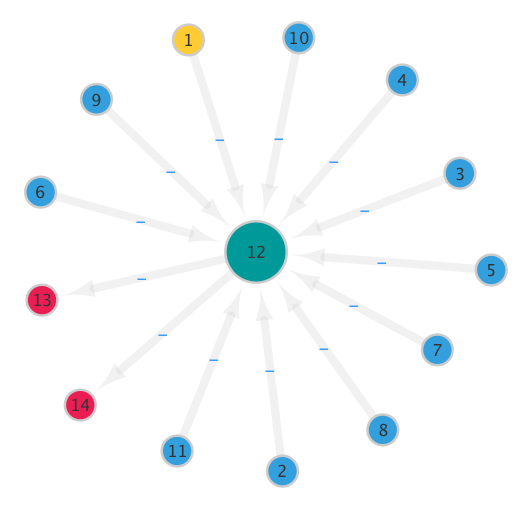
The input neurons has following numbers on the diagram above:

• Range Finders: #2 — RIGHT, #3 — FRONT-RIGHT, #4 — FRONT, #5 — FRONT-LEFT, #6 — LEFT, #7 — BACK
• Radar Sensors: #8 — FRONT, #9 — LEFT, #10 — BACK, #11 — RIGHT

> The Novelty Search metric definition for a maze environment

The Novelty Search optimization method is based on novelty metric calculation for each solver agent after performing a certain number of time steps in simulation of maze navigation for that agent. The novelty metric biases the search in a fundamentally different way than the objective-based fitness function (which depends only on the distance from the agent to the exit) and determines the behavior-space through which the search will be performed. Therefore, since what is important in the maze, this is where the solving agent ends navigation, then for the maze domain, the behavior of a navigator is defined as its final position. The novelty metric then maximizes the N-nearest neighbor distance⁴ between the final positions of all known solving agents, i.e. the most distant agent will have the greatest score of the novelty metric.

The effect of this novelty metric is to reward the solver agent for ending in a place where none have ended before and the method of traversal is ignored. This measure reflects that what is important, is to reach a certain location (i.e. the goal) rather than the method of locomotion. Thus, although the novelty metric has no knowledge of the ultimate goal, a solution that reaches the goal can appear novel. In addition, the comparison between fitness-based and novelty-based search is fair because both scores are calculated only based on the distance of the final position of the agent from other points.

EXPERIMENT RESULTS

As for deceptive environments we choose two types of maze environments with different complexity as was recommended in this research⁵: medium and hard maze. The maze configurations was designed in such a way as to create many cul-de-sacs with strong local optima, deceiving the objective-based optimization methods.

The Medium Complexity Maze Environment

The first experiment to establish baseline performance metric was performed using maze configuration of medium complexity. The Novelty Search optimization was combined with Neuro-Evolution of Augmented Topologies algorithm which use genetic neuro-evolution process to create a population of organisms capable of solving a maze. We also compared its performance with the objective-based optimization method for the NEAT algorithm, where fitness function optimization was dependent on how close final destination of produced organism is from the exit of the maze.

The final performance metric of each Autonomous Agent created for both optimization methods depends only on how close to the maze exit is the final destination of the solver after $400$ stimulation steps. Thus, despite the various methods of fitness function optimization, the final results can be compared for both methods. Each experimental trial was performed with $2000$ epochs of evolution or until a winner is found.

> Novelty Search Optimization

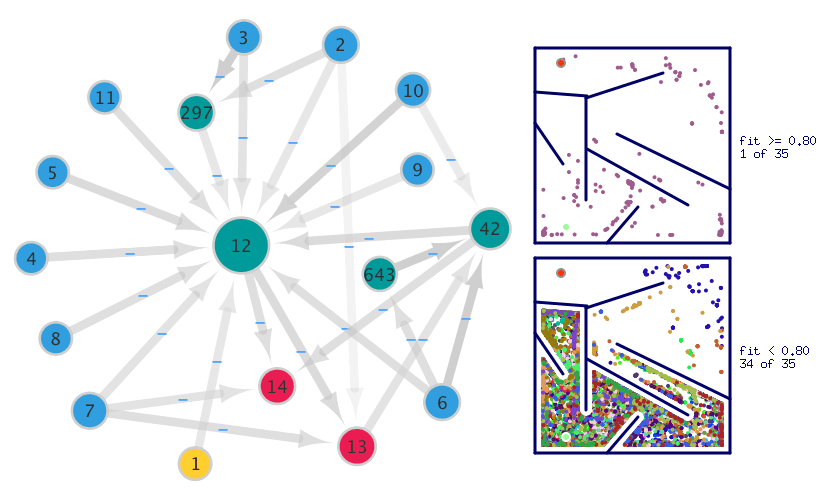
Applying Novelty Search based optimization it was possible to get the winner in 10 form 10 trials with optimal genome found approximately within $50$ generations. An Artificial Neural Network produced by an organism with a near optimal genome has $1$ neurons with only three hidden units, i.e. it was capable of growing two additional units compared to the above-mentioned seed genome (see Figure 2). And it is able to control maze solver agent with a spatial error of about $1.9%$ for targeting the exit of the maze.

Among with the two additional hidden units (neurons), the recurrent link was developed at the output neuron #13 (angular velocity effector) — see Figure 3. The recurrent link at this output neuron appears to be of great importance, since it was introduced in each configuration of the winner’s genome generated in each test trial. Such a consistent pattern seems pretty reasonable for the neuron #13, because it affects the agent’s steering and requires learning more complicated behavior compared to the neuron #14 (linear velocity control).

It is also interesting to consider the hidden neuron #91, which seemingly have learned the complex behavior of the steering to the exit of the maze when it is discovered to the right or behind the agent. We’ve made such assumptions because of its connections with input sensors #2, #7 (range finders: RIGHT, BACK) and #10, #11 (radar sensors: BACK, RIGHT).

The hidden neuron #293 connected with input sensor #11 (radar sensor: RIGHT), has learned to influence the steering of the agent in the direction of the exit of the maze, since most of the time the exit is on the right bottom relative to the agent.

The hidden neuron #12 which is introduced in seed genome operates as main control-and-relay switch relaying signals from sensors and other hidden neurons to the effectors (neurons #13, #14).

On the Figure 4 presented a diagram of the maze solving simulation by solver agents controlled by ANNs, derived from the genomes of all organisms introduced into the population until a winner is found. Agents are coded by color depending on which species the source organism belongs to. The fitness of agent is measured as the relative distance between its final destination and maze exit after running simulation for certain number of time steps ($400$ in our setup).

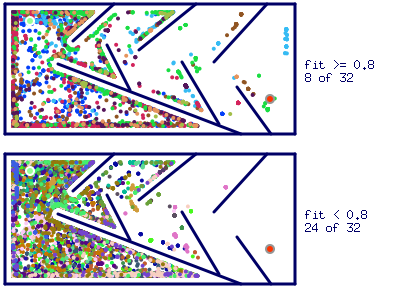
The initial agent position is at the top-left corner marked with green circle and maze exit at the bottom-right marked with red circle.

The upper plot shows the final destinations of the most fit agents ($fitness >= 0.8$), and the lower plot - the rest. The results are presented for an experimental trial producing the configuration of the winner genome depicted at Figure 3. The total number of species created at that trial is $32$, with only $8$ becoming the most fit ones ($fitness >= 0.8$).

> Objective-Based Optimization

Applying objective-based optimization, it was possible to create the winners capable of solving medium maze configuration in 9 from 10 trials. But the configuration of the winner’s genome in most cases was not so elegant and energy efficient, as with above-mentioned Novelty Search optimization.

After $248$ generations, it was found near optimal configuration of the winner’s genome (see Figure 5), capable of guiding the maze solving agent through the medium-complexity maze and reach the exit of the maze with spatial error about $1.8%$. The artificial neural network produced by this genome has $22$ units (neurons) with nine hidden neurons for modeling complex learned behavior.

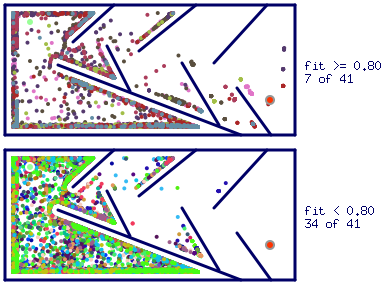
Comparing the objective-based simulation plot (Figure 6) with the similar for simulation based on Novelty Search optimization, it can be seen that agents final destinations are distributed less evenly through the maze space. Another interesting point is that most fit agents were less exploratory, moving mainly along the maze walls towards the local fitness optima. This behavior resulted in more generations needed to produce the winner on average, as well as completely failed trials.

The Hard Complexity Maze Environment

The hard maze configuration introduces additional complexity, emphasizing the idiosyncrasies of the objective-based optimization method. This requires a bit of strategic thinking, which sometimes allows the agent to deviate from the seemingly optimal places (with high local fitness function values) to finally find the guiding path through the maze. The ability of Novelty Search optimization to mimic mentioned strategic reasoning due to its inherent ability to find all the promising areas of the search space has made it an absolute champion with this experiment.

> Novelty Search Optimization

The Novelty Search optimization method, produced solving agents capable to solve the hard maze in 10 from 10 trials. The power of NS method led to the finding of winning solvers within up to $100$ generations in the maze environment of both: medium and hard complexity. Which marks NS as a highly effective optimization method for creating Autonomous Artificial Intelligent Agents capable of complex spatial navigation.

After $109$ generations of populations of organisms, the near optimal configuration of the winner’s genome was found (see Figure 7). The winner is able to guide the agent through the hard maze environment and approach the exit with a spatial error $2.5%$. The Artificial Neural Network produced by this genome has only $17$ units (neurons) with four hidden neurons for modeling complex learned behavior.

It is interesting to note that recurrent link on the output neuron #13 (angular velocity effector) was routed through two hidden neurons compared with the medium maze, where the neuron #13 was simply linked to itself. This may result in more complex behavior learned, especially taking into account that link passes through the neuron #42, affected by the range finder: LEFT and the radar: BACK. The neuron #42 is also affected by connection to the neuron #643 (affected by the range finder: LEFT). As a result, we can assume that it learned how to steer the agent when the exit of the maze is behind, and the wall is on the left, i.e. follow the left wall, moving forward.

Another important point to consider is about possible learned behavior encoded in the hidden neuron #297, which is affected by input range finder sensors detecting distance to obstacles in the RIGHT and FRONT direction. Considering the maze configuration, we can assume that this neuron learned to avoid the left chamber’s trap, where an extremely strong local maximum of the fitness function was introduced (based on the distance to the exit of the maze).

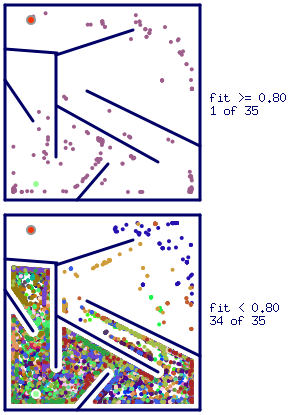
Because of the inherent complexity of the hard maze environment, only one species from $35$ was able to beget genome with fitness greater than $0.8$. This genome is also the winner able to produce control ANN successfully guiding solver agent to the exit of the maze. But, as can be seen from the Figure 8, there is a high probability that as the number of simulation steps increases, a larger number of species will be able to hit the fitness threshold ($0.8$).

> Objective-Based Optimization

The objective-based fitness function optimization method completely failed to create any successful solver agent within all 10 experiment trials. In some trials, it was able to create AAIAs, almost finding the exit of the maze, but it seems that many more simulation steps are required to eventually produce the winner genome, which makes it too computationally expensive.

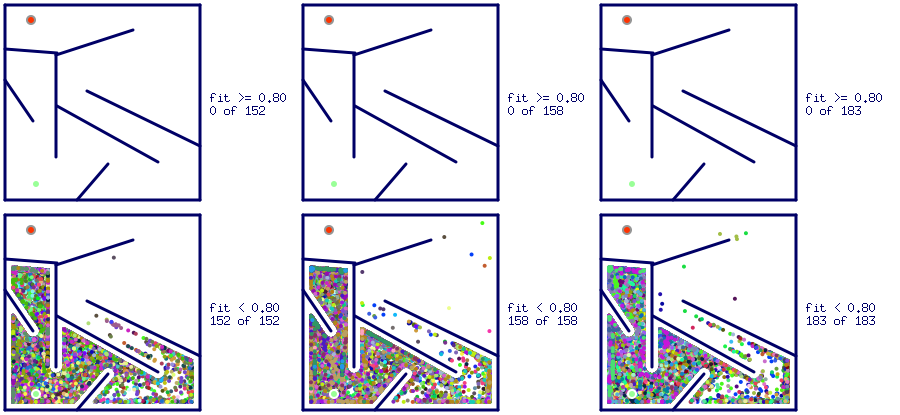
The Figure 9 depicts the most successful trials of the hard maze solvers with objective-based optimization of the fitness function. Looking at it, it can be seen that most of the final destinations of the Intelligent Agents were trapped in deceptive cul-de-sacs, blocking them from further exploration of the maze environment search space.

DISCUSSION

As shown by our experimental data, the Novelty Search method of fitness function optimization, when the fitness of the agent is based on the novelty of the solution that it was able to find, significantly outperforms traditional objective-based optimization and was even able to solve the navigation task when the traditional method failed completely.

We believe that Novelty Search optimization can be successfully applied to create optimal solving agents in many areas where strong deceptive local optima of fitness function prevents traditional objective-based methods from finding optimal or any solutions at all.

The full source code of the experiment implemented in GoLang: https://github.com/yaricom/goNEAT_NS. Please refer to it for more details about experiment particulars.

The associated research project can be found at ResearchGate: https://www.researchgate.net/project/Novelty-Search-optimization-for-NeuroEvolution

The author’s NEAT algorithm implementation in the GO language is also shared through NEAT software catalog, hosted by Evolutionary Complexity (EPlex) Research Group at the University of Central Florida: http://eplex.cs.ucf.edu/neat_software/

Special thanks to Dr. Kenneth O. Stanley for advises and sharing the NEAT algorithm details.

FUTURE WORK

We consider the development of modular AI systems based on ensembles of highly optimized compact Neural Networks. Our goal is to create compact utility NN blocks that are trained to represent vocabulary of the real-world terms that can be combined to form complex knowledge and skill sets. The mentioned NN blocks will be created using neuro-evolutionary algorithms by the method of gradual complexification, creating small and energy-efficient NN topologies that can be executed on a commodity CPUs with minimal power consumption. We call these blocks as Term Artificial Neural Network (tANN) to emphasize the fact that each NN block represents a specific term in our custom real-world vocabulary.

In addition, in order to model a more complex behavior, the Supervisor ANN (sANN) structure will be created to process the output of the tANN units and combine them with a common knowledge of the internal functions of the supervised process or system component.

It is assumed that Autonomous Artificial Intelligent system will be represented in the form of a complex hierarchy of tANN and sANN blocks in combination. Where each block or hierarchy of blocks will be responsible for a particular function, knowledge unit or set of the system skills. Such a modular / hierarchical approach provides a simple means to increase system capacity by introducing additional blocks with specific training. It is also possible to obtain an understanding of the flow of AI system reasoning, following the activations of its constituent blocks. The knowledge transfer also becomes easier by simply taking a NN block trained for a specific vocabulary term and introducing it into the new system.

> Our roadmap for future research

1. Creating definitions of the basic vocabulary terms
2. Creation of configurations of the seed genomes for each specific term of the vocabulary
3. Training / breeding of tANN structures from the vocabulary
4. Experiments on training / breeding of sANN-structures, capable of solving specific complex problems
5. Comparison of the performance of AI agents obtained using the described modular architecture against AI agents trained through traditional methods deep learning methods

References: